A Tight (3/2 + ε)-Approximation Algorithm for Demand Strip Packing

摘要

第一段简述 DSP 和 SP 的定义和目的，简要介绍二者的 NP-Hard 本质。

第二段引入本文发现的解的结构结论，并针对该结论提出本文的解决方案：在两种结构特征下分别运行对应的算法，取其中最优的结果。该算法可以得到 $(\frac{3}{2}+\varepsilon)OPT$ 的近似保证。

1 引言

1.1 研究问题

1.1.1 需求条带包装（DSP，Demand Strip Packing）

• 给定：

  • 一个包含 $n$ 个项目（工作）的集合 $\mathcal{I}={1,…,n}$ 和一个宽度 $D$（截止时间） 。每个项目 $i∈I$ 都有一个宽度（处理时间）$w(i)$ 和一个高度（需求）$h(i)$ 。

• 定义：

  • 一个D-可行的包装 (D-feasible packing)是一个分配函数 $σ:I→[0,D]$，它为每个项目 $i$ 指定一个开始时间 $σ(i)$，满足 $0≤σ(i)≤D−w(i)$，即所有项目都在时间 $0$ 或之后开始，并在截止时间 $D$ 之前结束 。
  • 对于一个给定的包装方案 $σ$ 和任意时间点 $t∈[0,D]$，我们将 $\mathcal{I}^σ(t)$ 定义为在 $t$ 时间点正在被处理的项目集合，即 $I^σ(t):={i∈I∣σ(i)≤t<σ(i)+w(i)}$。

• 目标：

  • 计算一个 D-可行的包装方案 $σ$，使其高度 $h(σ)$ 最小化，其中 $h(\sigma)=max_{t\in[0,D]}\Sigma_{i\in\mathcal{I}^\sigma(t)}h(i)$ 。该高度被定义为所有时间点中，并行处理的项目需求总和的最大值，即峰值需求 。

1.1.2 条带包装（SP，Strip Packing）

在这个问题中，给定一个宽度为 $D$、高度无限的轴对齐半条带以及一组轴对齐的开矩形，其中每个矩形i的宽度 $w(i) ∈(0,D]$ ，高度 $h(i) > 0$ 。在SP中的目标是在条带中计算所有矩形的轴对齐（任务矩形本身在调度条带中是网格对齐的）且不重叠的包装，同时最小化由矩形覆盖的最大高度。

1.1.3 二者的关系

条带包装（SP）是需求条带包装（DSP）的子问题，换言之，SP 的可行解集合是 DSP 可行解集合的一个子集（没错，虽然 DSP 的名字多两个字，但是它的条件上是更宽松的）。原因在于在很多的实际应用场景中，DSP 会伴随很多抢占式调度场景，所以二者在可否抢占调度上存在区别，换言之，即是否需要保持任务各个部分在纵轴方向上的对齐，抢占式调度往往意味着任务 $i$ 在纵轴方向上是可以“随时上下移动”的。

1.2 近似比的理论分析

该部分的理论分析引用自发表于 2014 IEEE International Conference on Smart Grid Communications 的文章 Peak Demand Scheduling in the Smart Grid

在 Eberle2024Packing 这篇文章中，引用部分提到如下叙述：一个简单的从划分问题中的规约表明，除非 P = NP，否则 SP 和 DSP都不能在 $\frac{3}{2}-ε$ 的因子内近似，对于任何 $ε>0$。对于这两个问题，SP和 DSP，目前最先进的是具有近似比率为 $\frac{5}{3}+ε$ 的算法。

1.2.1 证明

【警告】本部分内容博主本人还没有完全弄懂，鉴于内容的非必要性，请批判阅读或跳过该部分

在文章 Yaw2014Demand 中，该部分是结论按照这样的思路进行证明的：

首先我们已知条件：除非 N = NP，否则任何在多项式时间内运行的算法，都不可能保证为 Bin-Packing (BP) 问题找到一个近似比好于 $\frac{3}{2}$​ 的解。所以我们只需要把 BP 的实例映射到 DSP 的实例即可，这样所有可以解决 DSP 的算法都可以用来解决 BP ，BP 的算法的瓶颈也就同样定义了 DSP 算法的瓶颈。

BP问题的背景是有一些大小为 $s_{i}\in(0,1]$ 的物品，以及一大堆大小为 1 的箱子，目标是用最少的箱子放下所有的物品，下文中我们默认使用 $p$ 表示使用的箱子数量。

对于一个 BP 的实例，为了方便想象，我们可以想象一下箱子是一个宽度为 $w$ 、长度恒为 1 的容器，物品是宽度为 $w$ ，长度为$s_{i}$ 的物品。我们把箱子的长边（恒为 1 的边）横放，然后把这 $p$ 个箱子摞起来，自然形成了一个时间范围为 $(0,1)$ 、峰值需求为 $p$ 的 PDM 实例。这样实例的映射的完成了，瓶颈也得以证明。

1.3 主要贡献

1.3.1 定理 1.1

定理1.1： 对于任意的ε>0，存在一个 $\frac{3}{2}+\varepsilon$ 近似算法用于 DSP 问题。

1.3.2 定理 1.2

文章的巧妙之处正在于此，文章提出并证明了下面的定理 1.2 。

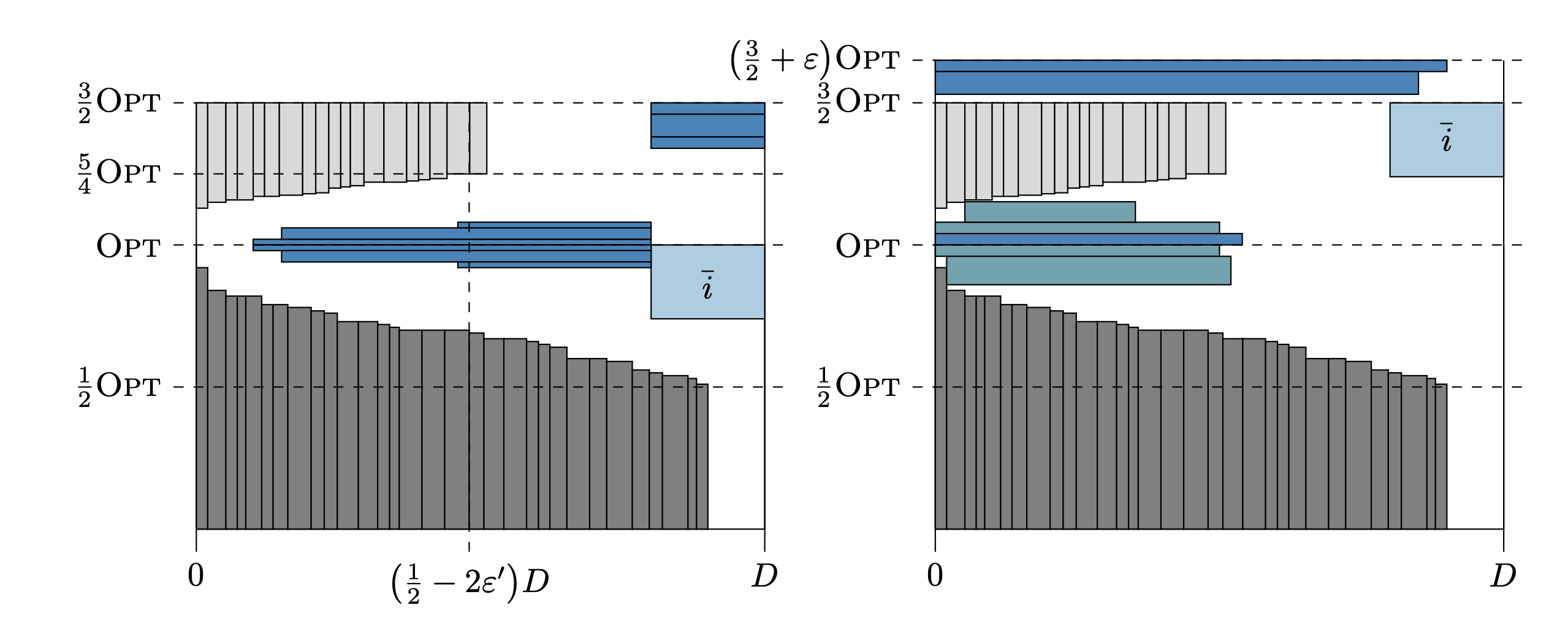
**任何最优包装都可以在 $\frac{3}{2}+\varepsilon$ 近似比的宽容下，转化为具有以下两种特定结构的包装 $\sigma$ ：

1. 整洁包装 $(\varepsilon,OPT)\text{-neat packing}$：从时间 0 开始，以非递增高度顺序将所有高度超过 OPT/2 的任务连续排列并打包。
2. 宽容包装 $\lambda\text{-forgiving packing}$：包装可以额外容纳一个高度最多为 3/2 OPT 、宽度为 $\lambda D$ 的任务（$\lambda<\varepsilon$）。

原文中对定理的形式化定义是：

对于任何 $\varepsilon>0$，任何 $\lambda\le min\lbrace\frac{\varepsilon}{3(5+4\varepsilon)}, \frac{1}{60}\rbrace$ ，以及任何实例 $(\mathcal{I},D)$ ，任何峰值调度为 OPT 的最优包装都可以被转化为一个是 $(\varepsilon,OPT)\text{-neat packing}$ 或 $\lambda\text{-forgiving packing}$ 的包装 $\sigma$ 。