Confocal non-line-of-sight imaging based on the light-cone transform

摘要

为藏在摄像机视域外的物品成像，是一个在很多研究领域非常重要且基础的问题。在很多领域都有应用潜力如机器人视觉、防御、遥感、自动驾驶等。宏观来讲，非视域成像（NLOS）可以用脉冲激光和时间分辨探测器扫描一个可见的表面得到测量数据。光探测与测距（LIDAR）系统利用此类测量从直接反射中恢复可见物体的形状，而 NLOS 成像是从多次散射的光中重建隐藏物体的形状和反照率。尽管近期取得了进展，但由于现有重建算法高昂的内存和处理需求，以及多次散射光信号极其微弱，NLOS 成像仍然不切实际。

在此，我们展示了一种共聚焦扫描程序可以通过简化光锥变换的推导来解决 NLOS 重建问题，从而应对这些挑战。该方法所需的计算和内存资源远小于以往的重建方法，并能以前所未有的分辨率对隐藏物体成像。在对逆反射物体成像时，共聚焦扫描还能大幅增加信号强度和探测距离。我们量化了 NLOS 成像的分辨率极限，展示了其在实时追踪方面的潜力，并推导出了能融合图像先验和物理精确噪声模型的高效算法。此外，我们还描述了在间接日光下成功的户外 NLOS 成像实验。

1 引言

1.1 相关系统：LIDAR 系统

LIDAR系统使用时间分辨传感器来扫描物体的三维（3D）几何结构。这类系统通过记录光从光源出发，沿直接路径到达物体上的一个点，再返回到传感器所需的时间来获取距离测量值。

最近，这些类型的传感器也被用于执行对“隐藏在拐角处”的物体进行NLOS追踪或成像，其中物体的位置和形状是通过间接光路计算出来的。

1.2 相关工作

对部分或完全被遮挡的物体进行成像这一挑战性任务，已有多种方法进行尝试：

1. 时间门控成像
2. 相干门控
3. 散斑相关
4. 波前整形
5. 鬼成像
6. 结构光
7. 强度成像

在宏观尺度上，最有前途的NLOS成像系统依赖于时间分辨探测器。

1.3 难点

1.3.1 NLOS 成像的难点

1. 沿间接路径传播的光在到达传感器之前会发生多次散射，并可能从相机直接视线范围之外的物体上发生散射。
2. 从间接光路中恢复隐藏物体的图像涉及一个具有挑战性的逆问题，因为需要考虑的此类路径有无限多条。

1.3.2 基于时间分辨探测器进行 NLOS 成像的难点

1. 重建步骤在内存需求和处理周期方面都具有令人望而却步的计算要求 。
2. 多次散射光的光通量极低，要么需要在黑暗环境中进行长时间的采集，要么需要足够高功率的激光来克服环境光的干扰。
3. NLOS成像通常需要一个由昂贵组件定制的硬件系统，从而阻碍了其广泛应用 。

1.4 解决方案：C - NLOS

作者提出的共聚焦NLOS（C-NLOS）成像旨在克服这些挑战 。

1.4.1 关键创新

以往的NLOS采集装置详尽地照亮并成像可见表面（如墙壁）上成对的不同点 ，而作者提出的系统则是照亮并成像同一点，并通过光栅扫描该点穿过墙壁来获取3D瞬态（即时间分辨）图像。

• 旧方法： 激光从A点打出去，探测器在B点接收。为了采全数据，需要测试大量的A-B点对组合。
• 共聚焦: 激光从A点打出去，探测器也在A点接收 。

1.4.2 优势

1. 它促进了NLOS问题闭式解的推导 。所提出的NLOS重建程序比以往方法快几个数量级，内存效率也更高，并且能产生更高质量的重建结果。
2. 共聚焦系统能够利用逆反射物体（如路牌、自行车反光片和高能见度安全服）的性质，显著增强间接信号。虽然对于漫反射物体，间接散射光仍然极其微弱。
3. LIDAR系统已经执行共聚焦扫描以从直接光路获取点云 。我们的原型系统是全新搭建的，但商业LIDAR系统可能只需最少的硬件修改就能支持这里开发的算法 。

1.5 基本假设

作者在这里提到，其他NLOS成像方法也采用类似的基本假设。

文中的图像形成模型做出以下基本假设：

1. 墙后只有单次散射（即场景的隐藏部分没有相互反射）
2. 光线各向同性散射（即模型忽略了朗伯余弦项）
3. 隐藏场景内没有遮挡发生 。

2 采样系统

文章的下一部分本来是紧接着的数学建模部分，但是博主在这里插入一个 Section 专门用来解释这个很重要的图 1。（事实上，文章只包含为数不多的四张图）

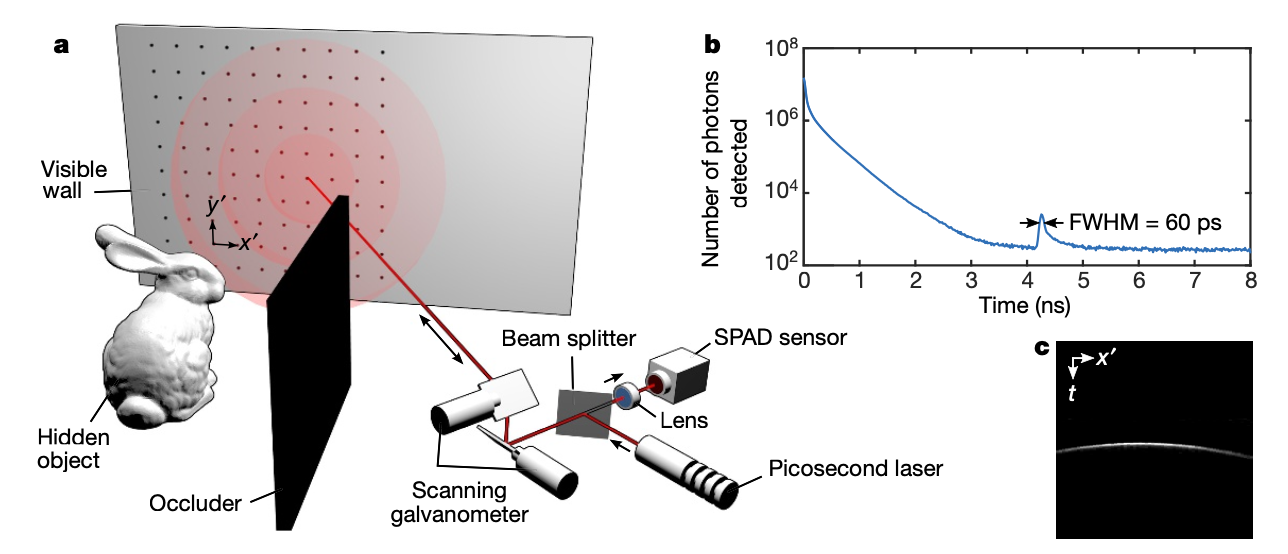
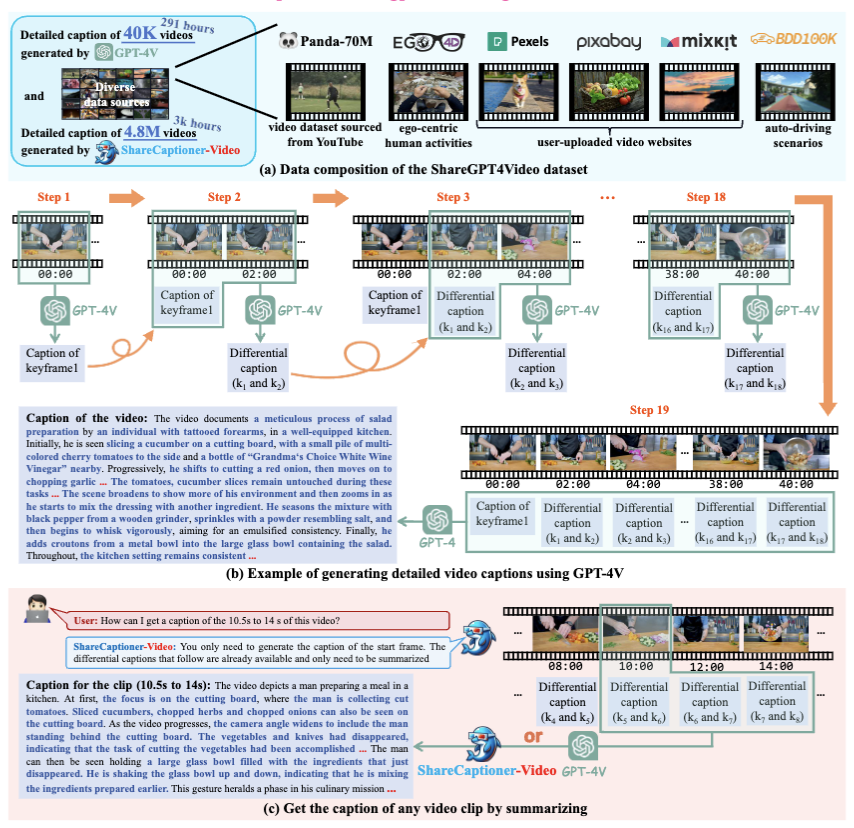
2.1 物理装置

1. 皮秒激光器 (Picosecond laser): 发射端。作为光源，发射持续时间极短的光脉冲。
2. SPAD sensor (单光子雪崩二极管): 接收端。一个极其灵敏的单光子探测器 。它的核心作用是以极高的时间精度（实验中时间分辨率的半峰全宽为60皮秒）记录下每一个光子到达的时刻。
3. 扫描振镜 (Scanning galvanometer): 控制激光束和探测器的朝向，使其能够在可见墙壁上进行精确、快速的光栅扫描。
4. 分束器 (Beam splitter): 巧妙地将发射光路和接收光路合并，确保激光发射点和信号接收点始终是墙上的同一点，这是实现“共聚焦”的关键。

2.2 数据处理

2.2.1 对点的表示

对应图 1b，是在墙上单个扫描点所采集到的数据。该数据表现为一个时间直方图，横轴是时间，纵轴是探测到的光子数量。

直方图上有两个关键信息：

• 在 $t=0$ 时刻的直接信号：一个巨大且尖锐的峰值，是激光直接从墙壁表面反射回来的信号。
• 在 $t > 0$ 时刻的间接信号：一个微弱的“回波”，是光线经由隐藏物体散射后返回的信号。这个信号的时间延迟直接对应于光线走过的额外路程（墙→物体→墙）。

2.2.2 对点列的表示

只需要把 2.2.1 部分中描述的单点时间直方图，沿着一条扫描线（例如 $x’$ 轴）并排拼接起来，就形成了图 1c，被称为条纹图像 (streak image)。

它的横轴是扫描位置 (x’)，纵轴是时间 (t)，图像亮度则代表光子数量。图中明亮的弧线轨迹，精确地捕捉了间接光传输的时空几何信息，这是重建算法赖以解码的核心数据。

2.2.3 对点面的表示

只需要把 2.2.2 部分中的“条纹图像”在面法线方向上（即 $y’$ 方向）进行叠放，形成一个立体的三维数据立方体。

这个数据立方体就是下文数学部分中，由共聚焦扫描点 $(x’, y’)$ 和时间 $t$ 构成的三维测量数据体 $τ$ 。它的三个维度分别是墙壁的 $x’$ 坐标、 $y’$ 坐标和时间t ，立方体中每个点的值就是该时空坐标上探测到的光子通量。

3 光锥变换

3.1 核心公式

2.2.3 中三维的测量数据体 τ 由公式 (1) 给出：

$$
\tau(x’,y’,t)=\iiint_{\Omega} \frac{1}{r^4} \rho(x,y,z) \delta(2\sqrt{(x’-x)^2+(y’-y)^2}+z^2-tc)dxdydz\qquad(1)
$$

τ(x’, y’, t):

测量结果。表示在墙上 $(x’, y’)$ 这个位置，于 $t$ 这个精确时刻，探测到的光子通量（可以理解为光的强度）。采集到的全部数据就是一个由无数个这样的 $τ$ 值构成的三维数据立方体。

∫∫∫:

表示 $\tau$ 是隐藏空间中所有点共同作用的结果。需要把隐藏空间中每一个点 $(x, y, z)$ 贡献的信号全部加起来，才能得到最终在墙上某一点的测量值。

ρ(x, y, z):

隐藏空间中 $(x, y, z)$ 点的反照率 (albedo)。反照率就是这个点的亮度或反射能力。作者通过测量到的 $τ$，反推出整个三维空间中 $ρ$ 的分布，从而“看到”隐藏的物体。

1/r⁴:

描述了信号强度的衰减规律。$r$ 是墙上的点到隐藏物体的距离。光从墙传播到物体，强度按 $1/r²$ 衰减，因此总的信号强度衰减是 $1/r⁴$。这个指数解释了为什么 NLOS 成像的信号极其微弱。

δ(…) (几何约束项 - 狄拉克δ函数):

这是公式中最核心也最巧妙的部分，它代表了物理定律的约束。括号里的表达式是 $2r - ct$ （ $r$ 是距离）。

$δ$ 函数的作用是：只有当括号内的表达式等于0时，它的值才不为零。

这个函数的物理意义是：只有当光走过的总路程精确等于“光速 × 飞行时间”时，我们才能在 $t$ 时刻探测到信号。它将时间和空间两个维度，通过光速这个物理常量，完美地联系在了一起。作者提到的闵可夫斯基光锥（Minkowski’s light cone），正是源自相对论，用于描述这种时空关系的经典几何模型 。

3.2 核心公式的性质

3.2.1 空间可变性

我们观察公式 (1) ，发现深度坐标 $z$ 和 $x$、$y$ 是通过平方和开根号的非线性关系耦合在一起的，而不是简单的差值关系，其在 $z$ 方向上，是典型的空间可变系统。此性质导致原公式无法通过简单的卷积操作求得解。

3.2.2 衰减项的可简化性

公式 (1) 存在一个特性：由于几何约束（狄拉克 $δ$ 函数），距离 $r$ 和时间 $t$ 是直接关联的。这意味着 ${1/r}^2$ 这个复杂的空间项，可以被看作是一个只与时间相关的系数，从而在数学上被简化处理。

作者特别指出了如何修改模型以适应逆反射材料：将衰减项从 ${1/r}^4$ 改为 ${1/r}^2$。它反映了物理现实：逆反射材料能将光线高效地原路返回，信号衰减慢得多，强度也因此大幅增加。

3.3 注意力惊人的变量代换

本节公式太难打了，博主就偷懒截图了，还请见谅

在论文对公式进行解释和分析后，作者突然提到可以通过“简单”的变量代换，消除模型中的空间可变性 (shift-variance)！

通过 $z=\sqrt{u}, dz/du= \frac{1}{(2\sqrt{u})}$ 和 $v=(tc/2)^2$ ，公式变成了下面的样子：

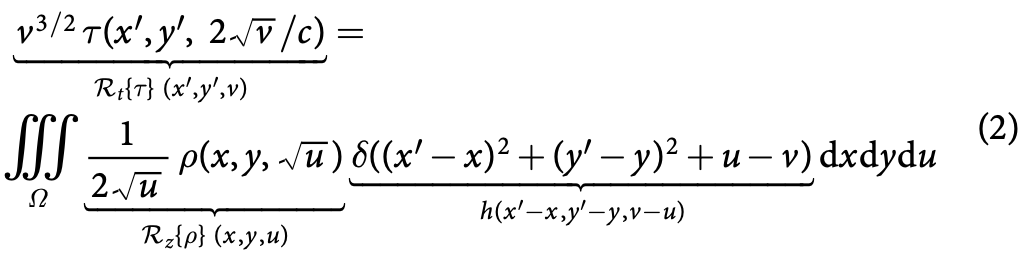
经过变量代换后，原本复杂的积分方程，神奇地变成了一个非常标准的三维卷积形式：

$$\mathcal{R}_t\lbrace\tau\rbrace=h*\mathcal{R}\lbrace\rho\rbrace$$

• $\mathcal{R}_t​$ 和 $\mathcal{R}_z$​ 代表了施加在测量数据 $τ$ 和真实场景 $ρ$ 上的坐标变换（即非均匀重采样）操作。
• $h$ 是一个空间不变的卷积核，它统一描述了系统在新坐标系下的模糊方式。
• $*$ 代表标准的卷积运算。

至此，整个从公式 (1) 到标准卷积形式的数学变换过程，被作者命名为光锥变换 (Light-Cone Transform, LCT)。

4 算法构建

4.1 离散化 LCT

将前文的连续卷积模型 $\mathcal{R}_t\lbrace\tau\rbrace=h*\mathcal{R}\lbrace\rho\rbrace$ 转换为离散的矩阵和向量形式 $\mathcal{R}_t\tau=H\mathcal{R}_z\rho$ 。

符号含义：

• $τ$ 和 $ρ$ 不再是函数，而是向量。
• $\mathcal{R}_t$, $\mathcal{R}_z$, $H$ 是矩阵 ，它们的作用就是对相应向量进行变换和卷积运算。

作者特别强调，这些矩阵运算都可以高效执行 。尤其是三维卷积 $H$ ，可以通过 FFT 在频域中飞速完成 ，这是整个算法能够快速运行的根本。

4.2 重建公式

通过将NLOS成像视为一个空间不变的三维反卷积问题，可以从卷积定理中推导出一个闭式解：原本在空间域中极其复杂的反卷积运算，在频率域中就变成了简单的逐元素除法。下面是重建最终解的算法公式：

$$
\rho_*=R_z^{-1}F^{-1}\left(\frac{1}{\widehat{H}} \frac{|\widehat{H}|^2}{|\widehat{H}|^2+ \frac{1}{\alpha} }\right)FR_t\tau
$$

括号内的部分是一个逆滤波器——维纳滤波器 (Wiener Filter)，当信号 $\widehat{H}$ 强时，它的作用近似于 $1 / \widehat{H}$ ，实现精确重建；当信号 $\widehat{H}$ 弱时，它会自动抑制该频率的输出，避免放大噪声。

4.3 算法可视化

文字和公式可能有些抽象，不过好在作者在论文的图 2 中非常直观地为我们展示了整个重建算法的过程。

整个重建流程可以清晰地分为三步，对应着图中 (a) 到 (d) 的演变：

1. (a → b) 时间轴重采样与校正

   • 输入(a): 算法的输入是我们通过采样系统得到的原始三维数据体 $τ$。从图中可以看到，它是一团模糊、弯曲的能量壳，这是隐藏物体回波信号在时空中的原始形态。
   • 变换(b): 算法的第一步是对 $τ$ 执行 $R_t$ 变换。这一步在数学上是坐标变换，在视觉上，它的作用就是将弯曲的能量壳 “拉直” ，它消除了空间可变性。

2. (b → c) 维纳滤波反卷积

   • 处理©: 对上一步校正后的数据应用维纳滤波器进行反卷积。在视觉上，这个过程就像是对焦，去除了环境噪声。此时，我们已经“看到”了物体，但它的几何形状仍然是处于被拉伸的变换空间中，看起来有点奇怪。

3. (c → d) 空间轴逆重采样与还原

   • 输出(d): 最后一步，算法执行 $R_z^{-1}$ 逆变换，将在变换空间中重建出的兔子“还原”回真实的三维物理空间。在视觉上，就是将在 © 中看到的、被拉伸的兔子恢复成其原始的、几何正确的形状。至此，我们便得到了最终的高质量重建结果 $ρ_*$ 。

5 性能分析

5.1 复杂度分析

• LCT算法复杂度： $O(N^3logN)$
• 传统反向投影算法复杂度： $O(N^5)$

5.2 现实世界实验

!

a,b 对比传统反向投影算法和本文的LCT算法，对室内一个隐藏的“Exit”逆反射路牌的重建效果。

c 在有间接日光（约100勒克斯）干扰的户外环境下，对一个隐藏的“S”形逆反射物体进行重建 。

5.3 分辨率极限

5.3.1 理论分析

作者给出了定义NLOS成像分辨率极限的理论公式，它揭示了成像精度受到哪些因素的制约：

$$
\Delta \mathcal{z}\le \frac{\mathcal{c\gamma}}{2}\quad and \quad \Delta x \le \frac{c\sqrt{w^2+z^2}}{2w}\gamma\qquad(4)
$$

• 轴向分辨率 (Δz): 指的是在深度方向分辨细节的能力。它仅取决于两个物理常量：光速 $c$ 和系统的时间精度 $γ$（即激光脉冲宽度和探测器响应时间）。

• 横向分辨率 (Δx): 指的是在水平和垂直方向分辨细节的能力 。它不仅取决于硬件时间精度 $γ$，还和几何设置 $w$（扫描墙面宽度的一半）和 $z$（隐藏物体的深度）有关。

换言之，在更大的墙面范围 ( $w$ ) 上扫描，也能获得更清晰的横向图像，这相当于构建了一个更大的“镜头”。

5.3.2 压力测试

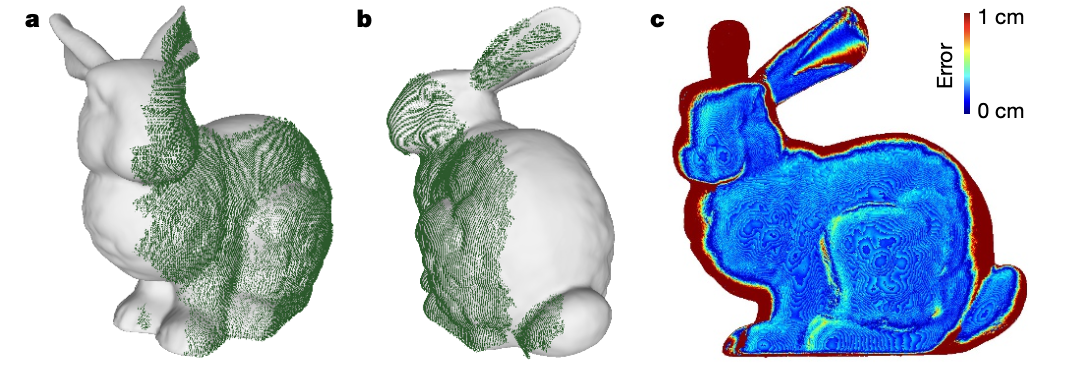
在 1024×1024×1024 体素的超高分辨率模拟中，LCT算法的重建结果与真实模型高度吻合，中位绝对误差仅为2.5毫米。

作者指出，如果用传统方法来解同样规模的问题，仅仅是存储其数学模型就需要超过 9 PB 的内存，这在计算上是完全不可能的。

但是LCT模型和当时所有的NLOS方法一样，无法处理隐藏场景内部的自遮挡问题。如图4所示，兔子左耳对右耳的遮挡导致了右耳部分重建失败。