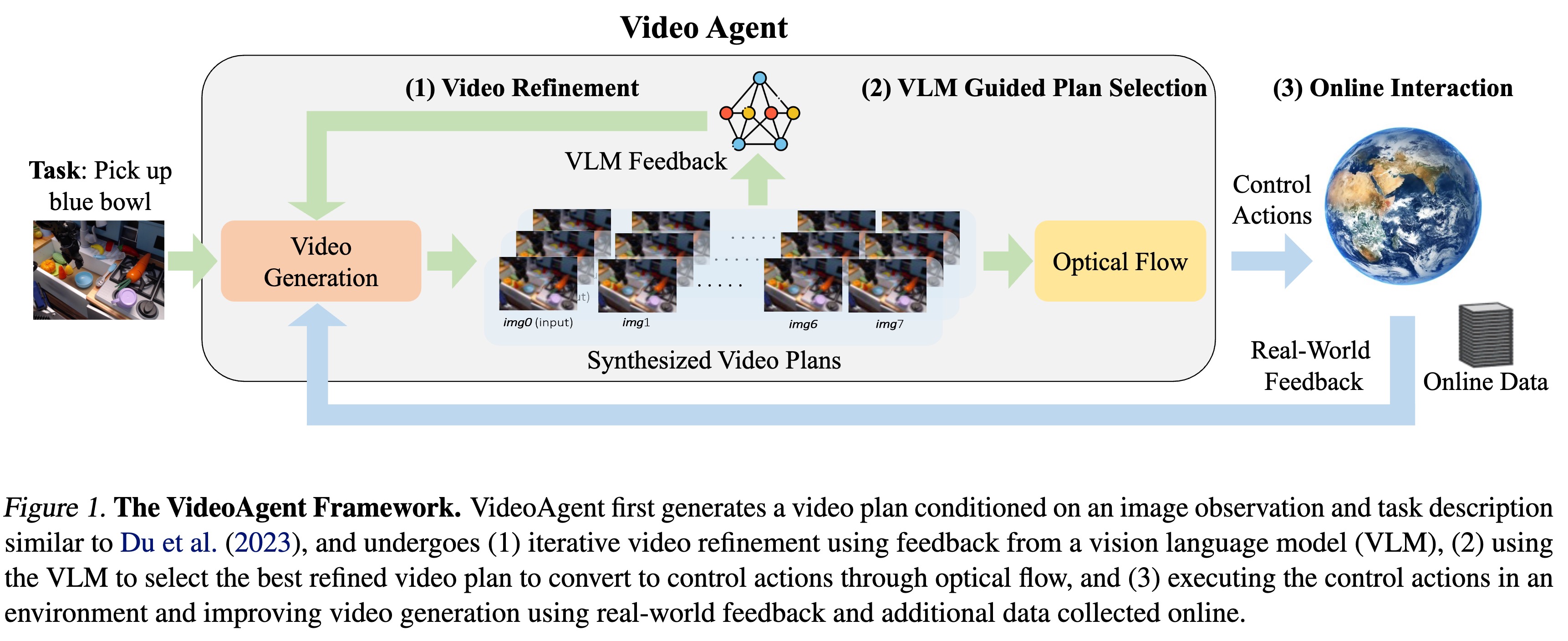
VideoAgent: Self-Improving Video Generation for Embodied Planning
基本信息
| 属性 | 内容 |
|---|---|
| 标题 | VideoAgent: Self-Improving Video Generation for Embodied Planning |
| 作者 | Achint Soni, Sreyas Venkataraman, Abhranil Chandra, Sebastian Fischmeister, Percy Liang, Bo Dai, Sherry Yang |
| 机构 | University of Waterloo, IIT Kharagpur, Stanford University, Georgia Tech, Google DeepMind, NYU |
| 来源 | 2025 arXiv: 2410.10076v3 |
| 总结 | 提出通过“自我调节一致性”机制,结合 VLM 反馈与在线环境交互,迭代优化视频生成策略以用于机器人规划 |
摘要
视频生成已被用于生成控制机器人系统的视觉计划(Visual Plans)。通常的做法是给定图像观测和语言指令,生成视频计划,然后将其转换为机器人控制指令并执行。然而,利用视频生成进行控制的一个主要瓶颈在于生成视频的质量,这些视频往往存在内容幻觉(Hallucinatory content)和不切实际的物理现象,导致从中提取控制动作时任务成功率低下。 虽然扩大数据集和模型规模是一个部分解决方案,但整合外部反馈对于将视频生成落地到物理世界既自然又至关重要。基于这一观察,我们提出了 VideoAgent,用于基于外部反馈自我改进生成的视频计划。VideoAgent 并不直接执行生成的视频计划,而是首先利用一种称为 自我调节一致性(Self-Conditioning Consistency) 的新颖程序来优化生成的视频计划,从而将推理时的计算量(Inference-time compute)转化为更好的生成质量。随着优化后的视频计划被执行,VideoAgent 还能从环境中收集额外数据,以进一步改进视频生成。在 MetaWorld 和 iTHOR 的模拟机器人操作实验中,VideoAgent 大幅减少了幻觉,从而提高了下游操作任务的成功率。我们进一步展示了 VideoAgent 可以有效优化真实机器人的视频,提供了机器人可以作为将视频生成落地物理世界的有效工具的早期证据。