ZeroFFa's Blog

摘要

第一段简述 DSP 和 SP 的定义和目的，简要介绍二者的 NP-Hard 本质。

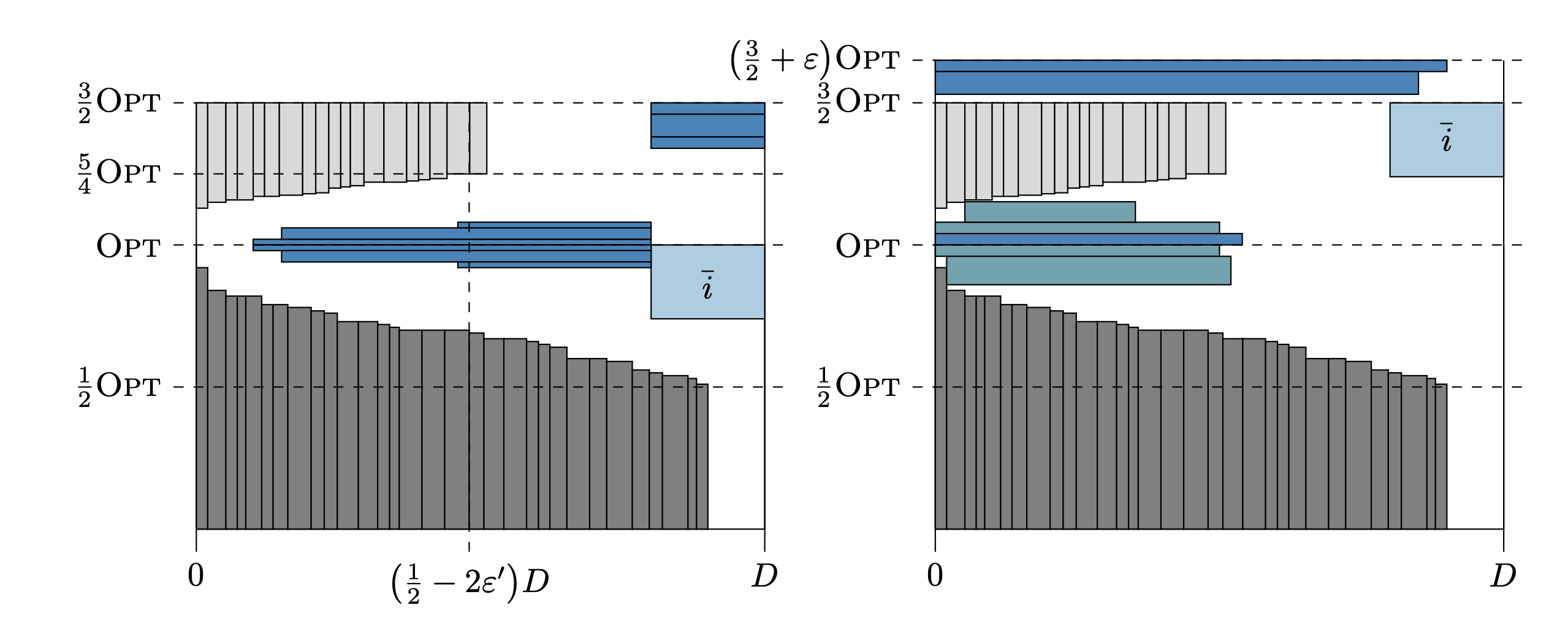
第二段引入本文发现的解的结构结论，并针对该结论提出本文的解决方案：在两种结构特征下分别运行对应的算法，取其中最优的结果。该算法可以得到 $(\frac{3}{2}+\varepsilon)OPT$ 的近似保证。

1 引言

1.1 研究问题

1.1.1 需求条带包装（DSP，Demand Strip Packing）

• 给定：

  • 一个包含 $n$ 个项目（工作）的集合 $\mathcal{I}={1,…,n}$ 和一个宽度 $D$（截止时间） 。每个项目 $i∈I$ 都有一个宽度（处理时间）$w(i)$ 和一个高度（需求）$h(i)$ 。

• 定义：

  • 一个D-可行的包装 (D-feasible packing)是一个分配函数 $σ:I→[0,D]$，它为每个项目 $i$ 指定一个开始时间 $σ(i)$，满足 $0≤σ(i)≤D−w(i)$，即所有项目都在时间 $0$ 或之后开始，并在截止时间 $D$ 之前结束 。
  • 对于一个给定的包装方案 $σ$ 和任意时间点 $t∈[0,D]$，我们将 $\mathcal{I}^σ(t)$ 定义为在 $t$ 时间点正在被处理的项目集合，即 $I^σ(t):={i∈I∣σ(i)≤t<σ(i)+w(i)}$。

• 目标：

  • 计算一个 D-可行的包装方案 $σ$，使其高度 $h(σ)$ 最小化，其中 $h(\sigma)=max_{t\in[0,D]}\Sigma_{i\in\mathcal{I}^\sigma(t)}h(i)$ 。该高度被定义为所有时间点中，并行处理的项目需求总和的最大值，即峰值需求 。